New Package for Energy-Based Sampling
Introducing EnergySamplers.jl
EnergySamplers.jl for energy-based sampling.
EnergySamplers
EnergySamplers.jl is a small and lightweight package for sampling from probability distributions using methods from energy-based modelling (EBM). Its functionality is used in other Taija packages, including JointEnergyModels.jl and CounterfactualExplanations.jl.
Extensions to Optimisers.jl
The package adds two new optimisers that are compatible with the Optimisers.jl interface:
- Stochastic Gradient Langevin Dynamics (SGLD) (Welling and Teh 2011) —
SGLD. - Improper SGLD (see, for example, Grathwohl et al. (2020)) —
ImproperSGLD.
SGLD is an efficient gradient-based Markov Chain Monte Carlo (MCMC) method that can be used in the context of EBM to draw samples from the model posterior (Murphy 2023). Formally, we can draw from \(p_{\theta}(x)\) as follows
\[ \begin{aligned} x_{j+1} &\leftarrow x_j - \frac{\epsilon_j^2}{2} \nabla_x \mathcal{E}_{\theta}(x_j) + \epsilon_j r_j, && j=1,...,J \end{aligned} \]
where \(r_j \sim \mathcal{N}(0,I)\) is a stochastic term and the step-size \(\epsilon_j\) is typically polynomially decayed (Welling and Teh 2011). To allow for faster sampling, it is common practice to choose the step-size \(\epsilon_j\) and the standard deviation of \(r_j\) separately. While \(x_J\) is only guaranteed to distribute as \(p_{\theta}(x)\) if \(\epsilon \rightarrow 0\) and \(J \rightarrow \infty\), the bias introduced for a small finite \(\epsilon\) is negligible in practice (Murphy 2023). We denote this form of sampling as Improper SGLD.
Example: Bayesian Inferecne with SGLD
To illustrate how the custom optimisers can be used, we will go through an example adapted from this (great!) blog post by Sebastian Callh. First, let’s load some dependencies:
Next, we load some data and prepare it for training a logistic regression model in Flux.jl:
Code
Random.seed!(2024)
data = dataset("ISLR", "Default")
todigit(x) = x == "Yes" ? 1.0 : 0.0
data[!, :Default] = map(todigit, data[:, :Default])
data[!, :Student] = map(todigit, data[:, :Student])
target = :Default
numerics = [:Balance, :Income]
features = [:Student, :Balance, :Income]
train, test = (d -> stratifiedobs(first, d; p=0.7))(shuffleobs(data))
for feature in numerics
μ, σ = rescale!(train[!, feature]; obsdim=1)
rescale!(test[!, feature], μ, σ; obsdim=1)
end
prep_X(x) = gpu(Matrix(x)')
prep_y(y) = gpu(reshape(y, 1, :))
train_X, test_X = prep_X.((train[:, features], test[:, features]))
train_y, test_y = prep_y.((train[:, target], test[:, target]))
train_set = Flux.DataLoader((train_X, train_y); batchsize=100, shuffle=false)Finally, we create a small helper function that runs the training loop for a given optimiser opt and number of steps:
Code
function train_logreg(; steps::Int=1000, opt=Flux.Descent(2))
Random.seed!(1)
paramvec(θ) = reduce(hcat, cpu(θ))
model = gpu(Dense(length(features), 1, sigmoid))
θ = Flux.params(model)
θ₀ = paramvec(θ)
predict(x; thres=0.5) = model(x) .> thres
accuracy(x, y) = mean(cpu(predict(x)) .== cpu(y))
loss(yhat, y) = Flux.binarycrossentropy(yhat, y)
avg_loss(yhat, y) = mean(loss(yhat, y))
trainloss() = avg_loss(model(train_X), train_y)
testloss() = avg_loss(model(test_X), test_y)
trainlosses = [cpu(trainloss()); zeros(steps)]
testlosses = [cpu(testloss()); zeros(steps)]
weights = [cpu(θ₀); zeros(steps, length(θ₀))]
opt_state = Flux.setup(opt, model)
for t in 1:steps
for data in train_set
input, label = data
# Calculate the gradient of the objective
# with respect to the parameters within the model:
grads = Flux.gradient(model) do m
result = m(input)
loss(result, label)
end
Flux.update!(opt_state, model, grads[1])
end
# Bookkeeping
weights[t + 1, :] = cpu(paramvec(θ))
trainlosses[t + 1] = cpu(trainloss())
testlosses[t + 1] = cpu(testloss())
end
println("Final parameters are $(paramvec(θ))")
println("Test accuracy is $(accuracy(test_X, test_y))")
return model, weights, trainlosses, testlosses
endNow we use this function to train the model, first using SGLD and then using Improper SGLD:
Code
results = train_logreg(; steps=100, opt=SGLD(10.0, 10.0, 0.9))
model, weights, trainlosses, testlosses = results
p1 = plot(weights; label=["Student" "Balance" "Income" "Intercept"], plot_title="SGLD")
results = train_logreg(; steps=100, opt=ImproperSGLD(2.0, 0.01))
model, weights, trainlosses, testlosses = results
p2 = plot(weights; label=["Student" "Balance" "Income" "Intercept"], plot_title="Improper SGLD")
plot(p1, p2, size=(800, 400))┌ Warning: Layer with Float32 parameters got Float64 input.
│ The input will be converted, but any earlier layers may be very slow.
│ layer = Dense(3 => 1, σ) # 4 parameters
│ summary(x) = "3×7000 adjoint(::Matrix{Float64}) with eltype Float64"
└ @ Flux ~/.julia/packages/Flux/vwk6M/src/layers/stateless.jl:59
Final parameters are Float32[-2.2376518 1.3661642 -1.7316573 -4.293961]
Test accuracy is 0.967
Final parameters are Float32[-0.5009609 2.7116675 0.09903357 -5.9262795]
Test accuracy is 0.9773333333333334The animation in Figure 2 shows the last 250 draws from the marginal posterior for each coefficient over the course of training using SGLD. The first 250 iterations are discarded. Not how the distributions tend to get more concentrated over the course of training as we approach convergence.
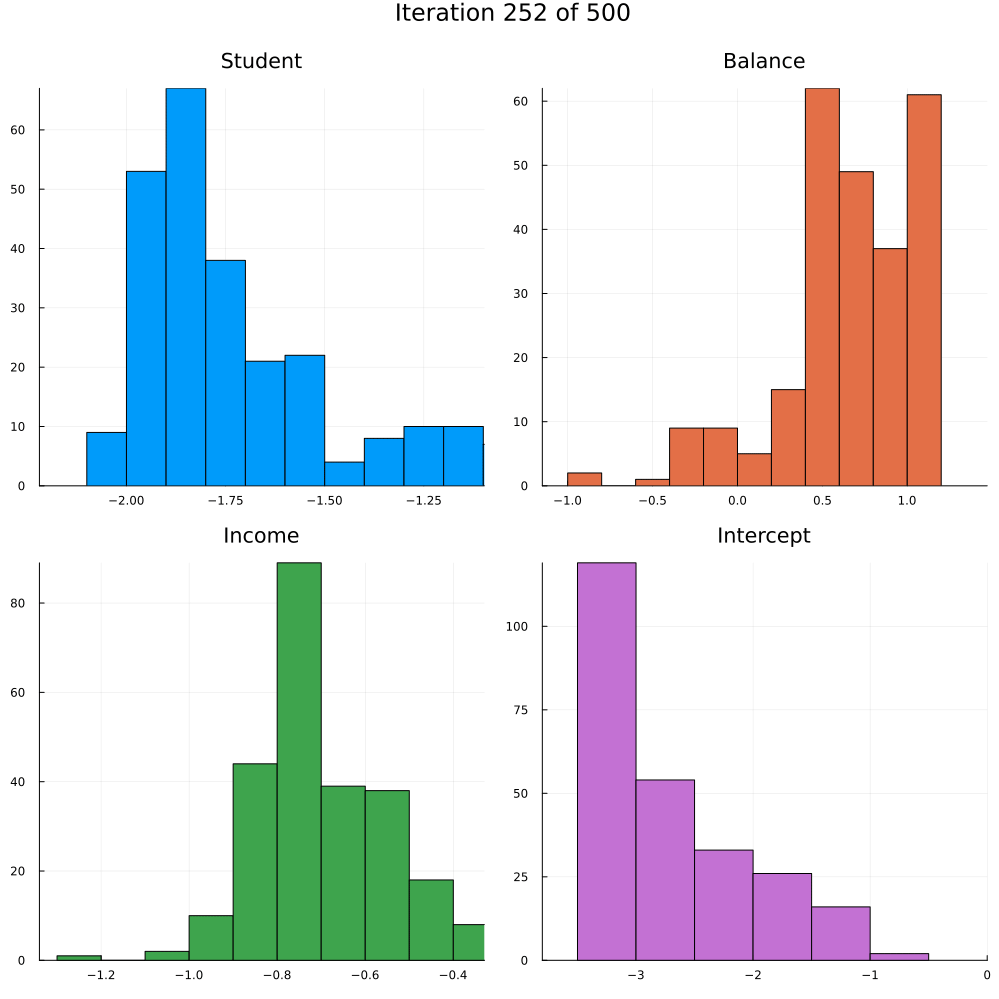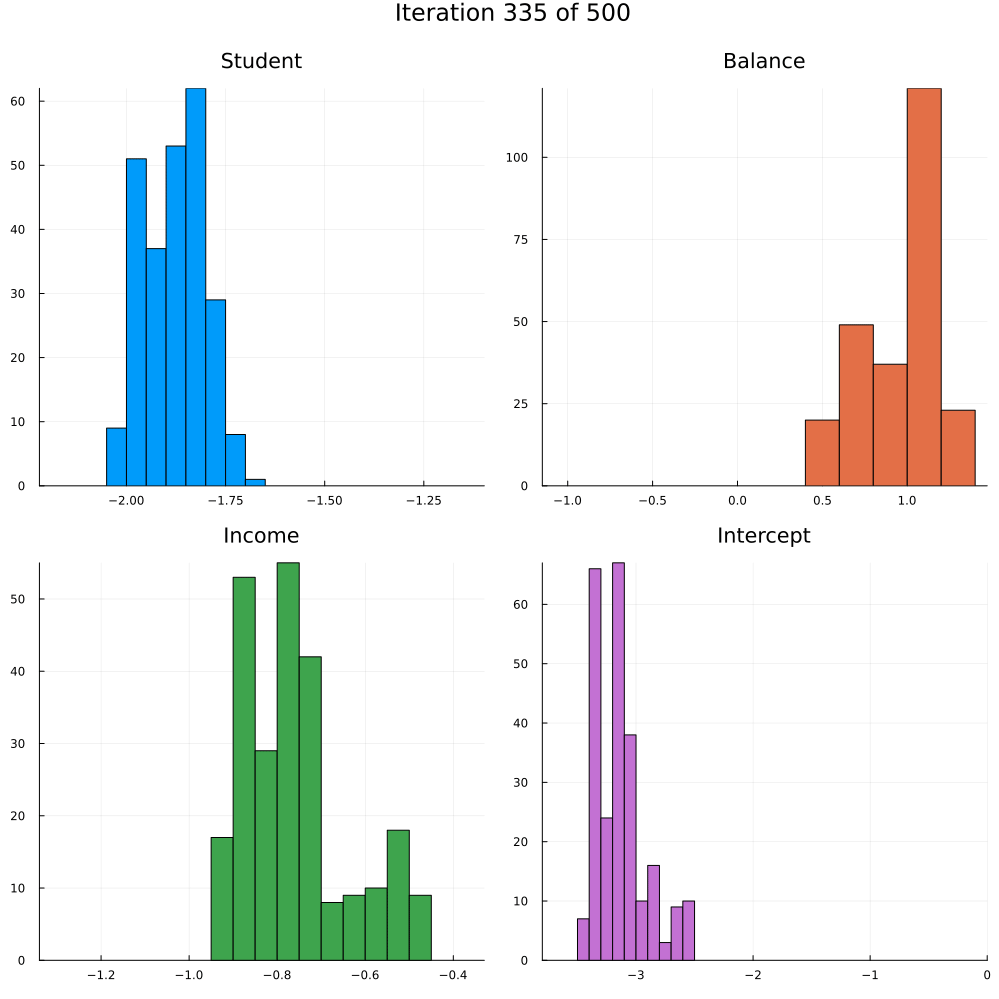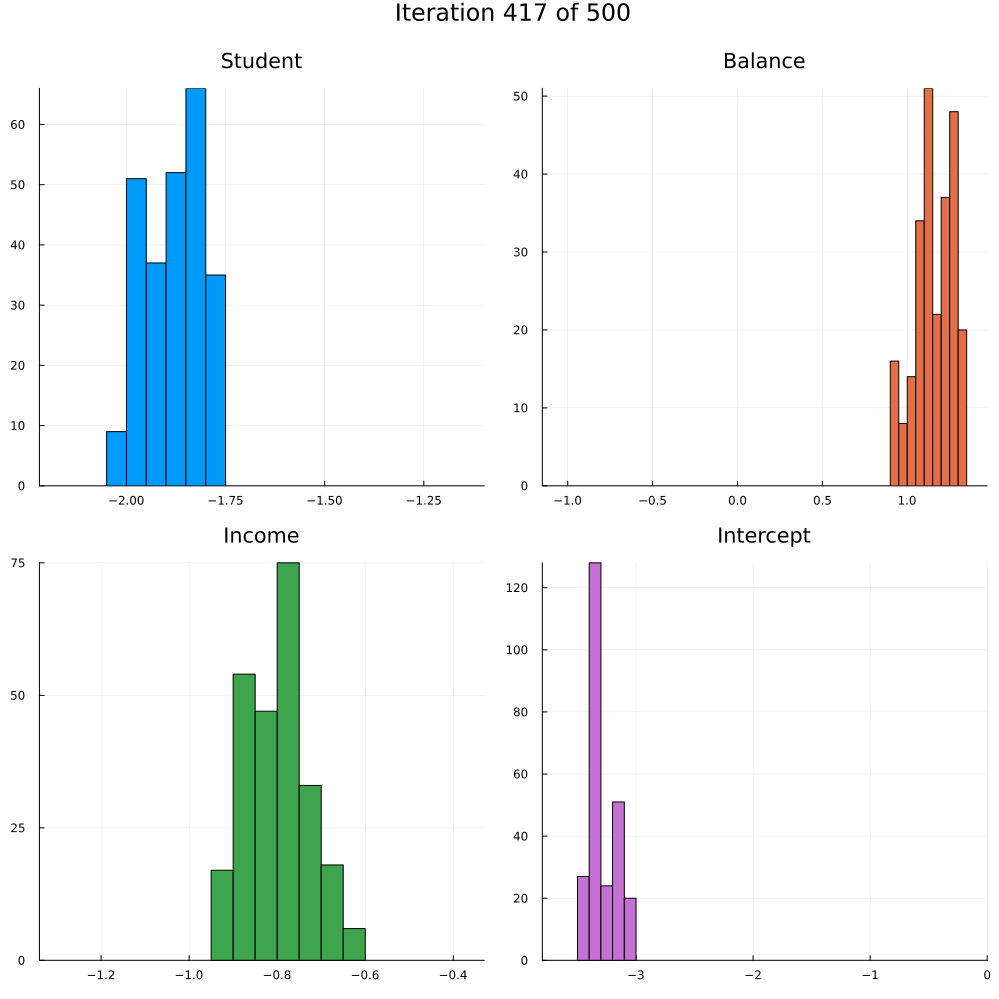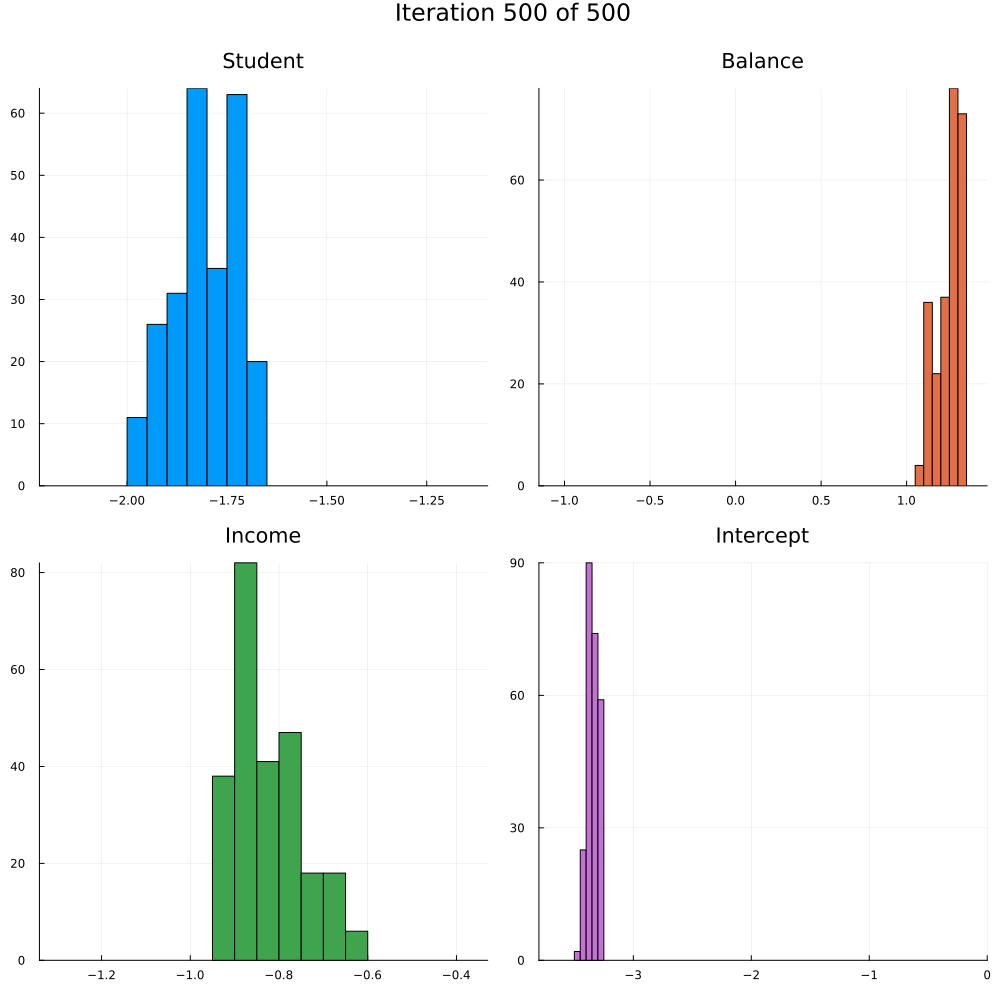
Energy-Based Samplers
In the context of EBM, the optimisers can be used to sample from a model posterior. To this end, the package provides the following samples:
UnconditionalSampler— samples from the unconditional distribution \(p_{\theta}(x)\) as in Grathwohl et al. (2020).ConditionalSampler— samples from the conditional distribution \(p_{\theta}(x|y)\) as in Grathwohl et al. (2020).JointSampler— samples from the joint distribution \(p_{\theta}(x,y)\) as in Kelly, Zemel, and Grathwohl (2021).
Example: Joint Energy-Based Model
The conditional sampler is used to draw class-conditional samples from a joint energy-based model (JEM) trained using Taija’s JointEnergyModels.jl. JEMs are explicitly trained to not only discriminate between output classes but also generate inputs. Hence, in the image below we can see that the model’s posterior conditional distributions (both over outputs and inputs) seem to approximate the true underlying distributions reasonably well: the model has learned to discriminate between the two classes (as indicated by the contours) and to generate samples from each class (as indicated by the stars).
Worked Example
Next, we will present a simple worked example involving linearly separable Gaussian blobs:
Code
We train a simple linear classifier to discriminate between output classes:
Code
# Train a simple neural network on the data (classification)
Xtrain = permutedims(MLJBase.matrix(X))
ytrain = Flux.onehotbatch(y, levels(y))
train_set = zip(eachcol(Xtrain), eachcol(ytrain))
inputdim = size(first(train_set)[1], 1)
outputdim = size(first(train_set)[2], 1)
nn = Chain(Dense(inputdim, outputdim))
loss(yhat, y) = Flux.logitcrossentropy(yhat, y)
opt_state = Flux.setup(Flux.Adam(), nn)
epochs = 5
for epoch in 1:epochs
Flux.train!(nn, train_set, opt_state) do m, x, y
loss(m(x), y)
end
@info "Epoch $epoch"
println("Accuracy: ", mean(Flux.onecold(nn(Xtrain)) .== Flux.onecold(ytrain)))
endFinally, we draw conditional samples from the model. Since we used a purely discriminative model for the task, the estimated posterior conditional distributions over inputs are not very good: the conditionally drawn samples (Xhat) largely lie on the right side of the decision boundary, but they are clearly not generated by the same data generating process as the training data.
Code
using EnergySamplers: ConditionalSampler, PMC
# PMC
bs = 10
ntrans = 10
niter = 100
# Conditionally sample from first class:
smpler = ConditionalSampler(
𝒟x, 𝒟y; input_size=size(Xmat)[1:(end - 1)], batch_size=bs
)
x1 = PMC(smpler, nn, ImproperSGLD(); ntransitions=ntrans, niter=niter, y=1)
# Conditionally sample from second class:
smpler = ConditionalSampler(
𝒟x, 𝒟y; input_size=size(Xmat)[1:(end - 1)], batch_size=bs
)
x2 = PMC(smpler, nn, ImproperSGLD(); ntransitions=ntrans, niter=niter, y=2)
# Contour plot for predictions:
xlims = extrema(hcat(x1,x2)[1,:]) .* 1.1
ylims = extrema(hcat(x1,x2)[2,:]) .* 1.1
xrange = range(xlims[1], xlims[2], 100)
yrange = range(ylims[1], ylims[2], 100)
z = [softmax(nn([x, y])) for x in xrange, y in yrange] |> z -> reduce(hcat, z)
plt = contourf(xrange, yrange, z[1,:], lw=0.1, xlims=xlims, ylims=ylims)
# Plot samples:
scatter!(Xtrain[1, :], Xtrain[2, :], color=Int.(y.refs), group=Int.(y.refs), label=["X|y=0" "X|y=1"], ms=2, markerstrokecolor=Int.(y.refs))
scatter!(x1[1, :], x1[2, :], color=1, label="Xhat|y=0", ms=4, alpha=0.5)
scatter!(x2[1, :], x2[2, :], color=2, label="Xhat|y=1", ms=4, alpha=0.5)
plot(plt)┌ Warning: Layer with Float32 parameters got Float64 input.
│ The input will be converted, but any earlier layers may be very slow.
│ layer = Dense(2 => 2) # 6 parameters
│ summary(x) = "2-element Vector{Float64}"
└ @ Flux ~/.julia/packages/Flux/vwk6M/src/layers/stateless.jl:59References
Citation
@online{altmeyer2024,
author = {Altmeyer, Patrick},
title = {New {Package} for {Energy-Based} {Sampling}},
date = {2024-09-06},
url = {https://www.taija.org/blog/posts/new-package-energysamplers/},
langid = {en}
}


